Data encryption standard (DES) | Set 1
This article talks about the Data Encryption Standard (DES), a historic encryption algorithm known for its 56-bit key length. We explore its operation, key transformation, and encryption process, shedding light on its role in data security and its vulnerabilities in today’s context.
What is DES?
Data Encryption Standard (DES) is a block cipher with a 56-bit key length that has played a significant role in data security . Data encryption standard (DES) has been found vulnerable to very powerful attacks therefore, the popularity of DES has been found slightly on the decline. DES is a block cipher and encrypts data in blocks of size of 64 bits each, which means 64 bits of plain text go as the input to DES, which produces 64 bits of ciphertext. The same algorithm and key are used for encryption and decryption , with minor differences. The key length is 56 bits .
The basic idea is shown below:
We have mentioned that DES uses a 56-bit key. Actually, The initial key consists of 64 bits. However, before the DES process even starts, every 8th bit of the key is discarded to produce a 56-bit key. That is bit positions 8, 16, 24, 32, 40, 48, 56, and 64 are discarded.

Thus, the discarding of every 8th bit of the key produces a 56-bit key from the original 64-bit key .
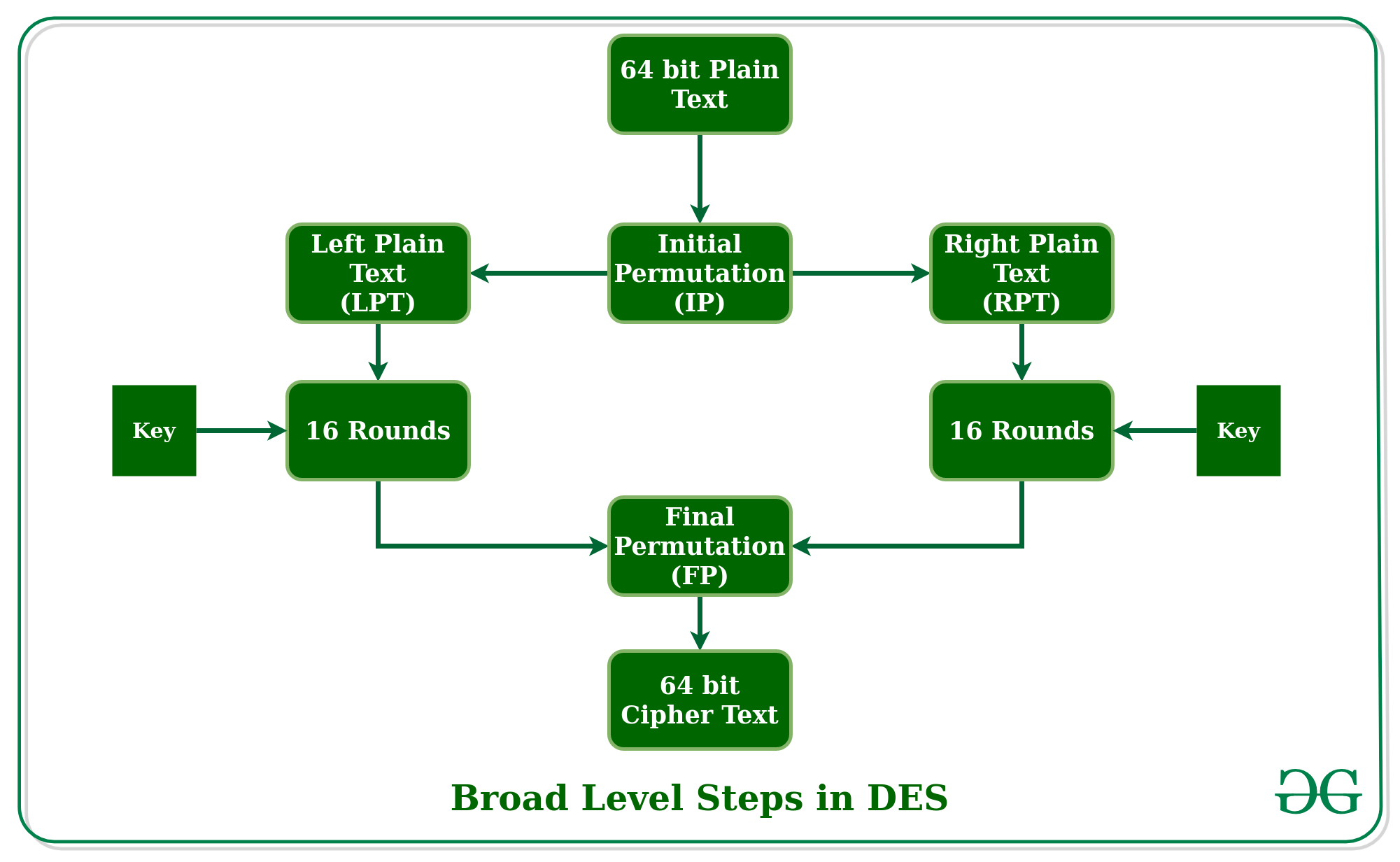
DES is based on the two fundamental attributes of cryptography : substitution (also called confusion) and transposition (also called diffusion). DES consists of 16 steps, each of which is called a round. Each round performs the steps of substitution and transposition. Let us now discuss the broad-level steps in DES.
- In the first step, the 64-bit plain text block is handed over to an initial Permutation (IP) function.
- The initial permutation is performed on plain text.
- Next, the initial permutation (IP) produces two halves of the permuted block; saying Left Plain Text (LPT) and Right Plain Text (RPT).
- Now each LPT and RPT go through 16 rounds of the encryption process.
- In the end, LPT and RPT are rejoined and a Final Permutation (FP) is performed on the combined block
- The result of this process produces 64-bit ciphertext.
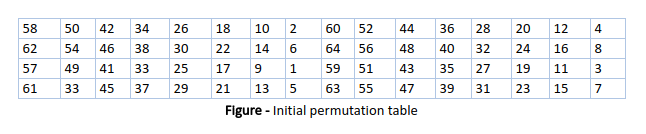
Initial Permutation (IP)
As we have noted, the initial permutation (IP) happens only once and it happens before the first round. It suggests how the transposition in IP should proceed, as shown in the figure. For example, it says that the IP replaces the first bit of the original plain text block with the 58th bit of the original plain text, the second bit with the 50th bit of the original plain text block, and so on.
This is nothing but jugglery of bit positions of the original plain text block. the same rule applies to all the other bit positions shown in the figure.
As we have noted after IP is done, the resulting 64-bit permuted text block is divided into two half blocks. Each half-block consists of 32 bits, and each of the 16 rounds, in turn, consists of the broad-level steps outlined in the figure.

Step 1: Key transformation
We have noted initial 64-bit key is transformed into a 56-bit key by discarding every 8th bit of the initial key. Thus, for each a 56-bit key is available. From this 56-bit key, a different 48-bit Sub Key is generated during each round using a process called key transformation. For this, the 56-bit key is divided into two halves, each of 28 bits. These halves are circularly shifted left by one or two positions, depending on the round.
For example: if the round numbers 1, 2, 9, or 16 the shift is done by only one position for other rounds, the circular shift is done by two positions. The number of key bits shifted per round is shown in the figure.

After an appropriate shift, 48 of the 56 bits are selected. From the 48 we might obtain 64 or 56 bits based on requirement which helps us to recognize that this model is very versatile and can handle any range of requirements needed or provided. for selecting 48 of the 56 bits the table is shown in the figure given below. For instance, after the shift, bit number 14 moves to the first position, bit number 17 moves to the second position, and so on. If we observe the table , we will realize that it contains only 48-bit positions. Bit number 18 is discarded (we will not find it in the table), like 7 others, to reduce a 56-bit key to a 48-bit key. Since the key transformation process involves permutation as well as a selection of a 48-bit subset of the original 56-bit key it is called Compression Permutation.

Because of this compression permutation technique, a different subset of key bits is used in each round. That makes DES not easy to crack.
Step 2: Expansion Permutation
Recall that after the initial permutation, we had two 32-bit plain text areas called Left Plain Text(LPT) and Right Plain Text(RPT). During the expansion permutation, the RPT is expanded from 32 bits to 48 bits. Bits are permuted as well hence called expansion permutation. This happens as the 32-bit RPT is divided into 8 blocks, with each block consisting of 4 bits. Then, each 4-bit block of the previous step is then expanded to a corresponding 6-bit block, i.e., per 4-bit block, 2 more bits are added.

This process results in expansion as well as a permutation of the input bit while creating output. The key transformation process compresses the 56-bit key to 48 bits. Then the expansion permutation process expands the 32-bit RPT to 48-bits . Now the 48-bit key is XOR with 48-bit RPT and the resulting output is given to the next step, which is the S-Box substitution .
Python
# Python3 code for the above approach
# Hexadecimal to binary conversion
def hex2bin(s):
mp = < '0' : "0000" ,
for i in range ( len (s)):
bin = bin + mp[s[i]]
return bin
# Binary to hexadecimal conversion
def bin2hex(s):
mp = < "0000" : '0' ,
for i in range ( 0 , len (s), 4 ):
ch = ch + s[i]
ch = ch + s[i + 1 ]
ch = ch + s[i + 2 ]
ch = ch + s[i + 3 ]
hex = hex + mp[ch]
return hex
# Binary to decimal conversion
def bin2dec(binary):
binary1 = binary
decimal, i, n = 0 , 0 , 0
while (binary ! = 0 ):
dec = binary % 10
decimal = decimal + dec * pow ( 2 , i)
binary = binary / / 10
return decimal
# Decimal to binary conversion
def dec2bin(num):
res = bin (num).replace( "0b" , "")
if ( len (res) % 4 ! = 0 ):
div = len (res) / 4
div = int (div)
counter = ( 4 * (div + 1 )) - len (res)
for i in range ( 0 , counter):
res = '0' + res
return res
# Permute function to rearrange the bits
def permute(k, arr, n):
permutation = ""
for i in range ( 0 , n):
permutation = permutation + k[arr[i] - 1 ]
return permutation
# shifting the bits towards left by nth shifts
def shift_left(k, nth_shifts):
for i in range (nth_shifts):
for j in range ( 1 , len (k)):
# calculating xow of two strings of binary number a and b
def xor(a, b):
for i in range ( len (a)):
if a[i] = = b[i]:
ans = ans + "0"
ans = ans + "1"
return ans
# Table of Position of 64 bits at initial level: Initial Permutation Table
initial_perm = [ 58 , 50 , 42 , 34 , 26 , 18 , 10 , 2 ,
60 , 52 , 44 , 36 , 28 , 20 , 12 , 4 ,
62 , 54 , 46 , 38 , 30 , 22 , 14 , 6 ,
64 , 56 , 48 , 40 , 32 , 24 , 16 , 8 ,
57 , 49 , 41 , 33 , 25 , 17 , 9 , 1 ,
59 , 51 , 43 , 35 , 27 , 19 , 11 , 3 ,
61 , 53 , 45 , 37 , 29 , 21 , 13 , 5 ,
63 , 55 , 47 , 39 , 31 , 23 , 15 , 7 ]
# Expansion D-box Table
exp_d = [ 32 , 1 , 2 , 3 , 4 , 5 , 4 , 5 ,
6 , 7 , 8 , 9 , 8 , 9 , 10 , 11 ,
12 , 13 , 12 , 13 , 14 , 15 , 16 , 17 ,
16 , 17 , 18 , 19 , 20 , 21 , 20 , 21 ,
22 , 23 , 24 , 25 , 24 , 25 , 26 , 27 ,
28 , 29 , 28 , 29 , 30 , 31 , 32 , 1 ]
# Straight Permutation Table
per = [ 16 , 7 , 20 , 21 ,
29 , 12 , 28 , 17 ,
1 , 15 , 23 , 26 ,
5 , 18 , 31 , 10 ,
2 , 8 , 24 , 14 ,
32 , 27 , 3 , 9 ,
19 , 13 , 30 , 6 ,
22 , 11 , 4 , 25 ]
# S-box Table
sbox = [[[ 14 , 4 , 13 , 1 , 2 , 15 , 11 , 8 , 3 , 10 , 6 , 12 , 5 , 9 , 0 , 7 ],
[ 0 , 15 , 7 , 4 , 14 , 2 , 13 , 1 , 10 , 6 , 12 , 11 , 9 , 5 , 3 , 8 ],
[ 4 , 1 , 14 , 8 , 13 , 6 , 2 , 11 , 15 , 12 , 9 , 7 , 3 , 10 , 5 , 0 ],
[ 15 , 12 , 8 , 2 , 4 , 9 , 1 , 7 , 5 , 11 , 3 , 14 , 10 , 0 , 6 , 13 ]],
[[ 15 , 1 , 8 , 14 , 6 , 11 , 3 , 4 , 9 , 7 , 2 , 13 , 12 , 0 , 5 , 10 ],
[ 3 , 13 , 4 , 7 , 15 , 2 , 8 , 14 , 12 , 0 , 1 , 10 , 6 , 9 , 11 , 5 ],
[ 0 , 14 , 7 , 11 , 10 , 4 , 13 , 1 , 5 , 8 , 12 , 6 , 9 , 3 , 2 , 15 ],
[ 13 , 8 , 10 , 1 , 3 , 15 , 4 , 2 , 11 , 6 , 7 , 12 , 0 , 5 , 14 , 9 ]],
[[ 10 , 0 , 9 , 14 , 6 , 3 , 15 , 5 , 1 , 13 , 12 , 7 , 11 , 4 , 2 , 8 ],
[ 13 , 7 , 0 , 9 , 3 , 4 , 6 , 10 , 2 , 8 , 5 , 14 , 12 , 11 , 15 , 1 ],
[ 13 , 6 , 4 , 9 , 8 , 15 , 3 , 0 , 11 , 1 , 2 , 12 , 5 , 10 , 14 , 7 ],
[ 1 , 10 , 13 , 0 , 6 , 9 , 8 , 7 , 4 , 15 , 14 , 3 , 11 , 5 , 2 , 12 ]],
[[ 7 , 13 , 14 , 3 , 0 , 6 , 9 , 10 , 1 , 2 , 8 , 5 , 11 , 12 , 4 , 15 ],
[ 13 , 8 , 11 , 5 , 6 , 15 , 0 , 3 , 4 , 7 , 2 , 12 , 1 , 10 , 14 , 9 ],
[ 10 , 6 , 9 , 0 , 12 , 11 , 7 , 13 , 15 , 1 , 3 , 14 , 5 , 2 , 8 , 4 ],
[ 3 , 15 , 0 , 6 , 10 , 1 , 13 , 8 , 9 , 4 , 5 , 11 , 12 , 7 , 2 , 14 ]],
[[ 2 , 12 , 4 , 1 , 7 , 10 , 11 , 6 , 8 , 5 , 3 , 15 , 13 , 0 , 14 , 9 ],
[ 14 , 11 , 2 , 12 , 4 , 7 , 13 , 1 , 5 , 0 , 15 , 10 , 3 , 9 , 8 , 6 ],
[ 4 , 2 , 1 , 11 , 10 , 13 , 7 , 8 , 15 , 9 , 12 , 5 , 6 , 3 , 0 , 14 ],
[ 11 , 8 , 12 , 7 , 1 , 14 , 2 , 13 , 6 , 15 , 0 , 9 , 10 , 4 , 5 , 3 ]],
[[ 12 , 1 , 10 , 15 , 9 , 2 , 6 , 8 , 0 , 13 , 3 , 4 , 14 , 7 , 5 , 11 ],
[ 10 , 15 , 4 , 2 , 7 , 12 , 9 , 5 , 6 , 1 , 13 , 14 , 0 , 11 , 3 , 8 ],
[ 9 , 14 , 15 , 5 , 2 , 8 , 12 , 3 , 7 , 0 , 4 , 10 , 1 , 13 , 11 , 6 ],
[ 4 , 3 , 2 , 12 , 9 , 5 , 15 , 10 , 11 , 14 , 1 , 7 , 6 , 0 , 8 , 13 ]],
[[ 4 , 11 , 2 , 14 , 15 , 0 , 8 , 13 , 3 , 12 , 9 , 7 , 5 , 10 , 6 , 1 ],
[ 13 , 0 , 11 , 7 , 4 , 9 , 1 , 10 , 14 , 3 , 5 , 12 , 2 , 15 , 8 , 6 ],
[ 1 , 4 , 11 , 13 , 12 , 3 , 7 , 14 , 10 , 15 , 6 , 8 , 0 , 5 , 9 , 2 ],
[ 6 , 11 , 13 , 8 , 1 , 4 , 10 , 7 , 9 , 5 , 0 , 15 , 14 , 2 , 3 , 12 ]],
[[ 13 , 2 , 8 , 4 , 6 , 15 , 11 , 1 , 10 , 9 , 3 , 14 , 5 , 0 , 12 , 7 ],
[ 1 , 15 , 13 , 8 , 10 , 3 , 7 , 4 , 12 , 5 , 6 , 11 , 0 , 14 , 9 , 2 ],
[ 7 , 11 , 4 , 1 , 9 , 12 , 14 , 2 , 0 , 6 , 10 , 13 , 15 , 3 , 5 , 8 ],
[ 2 , 1 , 14 , 7 , 4 , 10 , 8 , 13 , 15 , 12 , 9 , 0 , 3 , 5 , 6 , 11 ]]]
# Final Permutation Table
final_perm = [ 40 , 8 , 48 , 16 , 56 , 24 , 64 , 32 ,
39 , 7 , 47 , 15 , 55 , 23 , 63 , 31 ,
38 , 6 , 46 , 14 , 54 , 22 , 62 , 30 ,
37 , 5 , 45 , 13 , 53 , 21 , 61 , 29 ,
36 , 4 , 44 , 12 , 52 , 20 , 60 , 28 ,
35 , 3 , 43 , 11 , 51 , 19 , 59 , 27 ,
34 , 2 , 42 , 10 , 50 , 18 , 58 , 26 ,
33 , 1 , 41 , 9 , 49 , 17 , 57 , 25 ]
def encrypt(pt, rkb, rk):
pt = hex2bin(pt)
# Initial Permutation
pt = permute(pt, initial_perm, 64 )
print ( "After initial permutation" , bin2hex(pt))
left = pt[ 0 : 32 ]
right = pt[ 32 : 64 ]
for i in range ( 0 , 16 ):
# Expansion D-box: Expanding the 32 bits data into 48 bits
right_expanded = permute(right, exp_d, 48 )
# XOR RoundKey[i] and right_expanded
xor_x = xor(right_expanded, rkb[i])
# S-boxex: substituting the value from s-box table by calculating row and column
for j in range ( 0 , 8 ):
row = bin2dec( int (xor_x[j * 6 ] + xor_x[j * 6 + 5 ]))
col = bin2dec(
int (xor_x[j * 6 + 1 ] + xor_x[j * 6 + 2 ] + xor_x[j * 6 + 3 ] + xor_x[j * 6 + 4 ]))
val = sbox[j][row][col]
sbox_str = sbox_str + dec2bin(val)
# Straight D-box: After substituting rearranging the bits
sbox_str = permute(sbox_str, per, 32 )
# XOR left and sbox_str
result = xor(left, sbox_str)
left = result
left, right = right, left
print ( "Round " , i + 1 , " " , bin2hex(left),
" " , bin2hex(right), " " , rk[i])
# Combination
combine = left + right
# Final permutation: final rearranging of bits to get cipher text
cipher_text = permute(combine, final_perm, 64 )
return cipher_text
pt = "123456ABCD132536"
key = "AABB09182736CCDD"
# Key generation
# --hex to binary
key = hex2bin(key)
# --parity bit drop table
keyp = [ 57 , 49 , 41 , 33 , 25 , 17 , 9 ,
1 , 58 , 50 , 42 , 34 , 26 , 18 ,
10 , 2 , 59 , 51 , 43 , 35 , 27 ,
19 , 11 , 3 , 60 , 52 , 44 , 36 ,
63 , 55 , 47 , 39 , 31 , 23 , 15 ,
7 , 62 , 54 , 46 , 38 , 30 , 22 ,
14 , 6 , 61 , 53 , 45 , 37 , 29 ,
21 , 13 , 5 , 28 , 20 , 12 , 4 ]
# getting 56 bit key from 64 bit using the parity bits
key = permute(key, keyp, 56 )
# Number of bit shifts
shift_table = [ 1 , 1 , 2 , 2 ,
2 , 2 , 2 , 2 ,
1 , 2 , 2 , 2 ,
2 , 2 , 2 , 1 ]
# Key- Compression Table : Compression of key from 56 bits to 48 bits
key_comp = [ 14 , 17 , 11 , 24 , 1 , 5 ,
3 , 28 , 15 , 6 , 21 , 10 ,
23 , 19 , 12 , 4 , 26 , 8 ,
16 , 7 , 27 , 20 , 13 , 2 ,
41 , 52 , 31 , 37 , 47 , 55 ,
30 , 40 , 51 , 45 , 33 , 48 ,
44 , 49 , 39 , 56 , 34 , 53 ,
46 , 42 , 50 , 36 , 29 , 32 ]
left = key[ 0 : 28 ] # rkb for RoundKeys in binary
right = key[ 28 : 56 ] # rk for RoundKeys in hexadecimal
for i in range ( 0 , 16 ):
# Shifting the bits by nth shifts by checking from shift table
left = shift_left(left, shift_table[i])
right = shift_left(right, shift_table[i])
# Combination of left and right string
combine_str = left + right
# Compression of key from 56 to 48 bits
round_key = permute(combine_str, key_comp, 48 )
rkb.append(round_key)
rk.append(bin2hex(round_key))
print ( "Encryption" )
cipher_text = bin2hex(encrypt(pt, rkb, rk))
print ( "Cipher Text : " , cipher_text)
print ( "Decryption" )
rkb_rev = rkb[:: - 1 ]
rk_rev = rk[:: - 1 ]
text = bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))
print ( "Plain Text : " , text)
# This code is contributed by Aditya Jain
Javascript
// Define DES key and plaintext
const key = "0123456789abcdef" ;
const plaintext = "Hello, world!" ;
// Perform DES encryption
const des = new DES(key);
const ciphertext = des.encrypt(plaintext);
// Perform DES decryption
const decrypted = des.decrypt(ciphertext);
// Print results
console.log( "Plaintext: " , plaintext);
console.log( "Ciphertext: " , ciphertext);
console.log( "Decrypted: " , decrypted);
// Define DES class
constructor(key) <
// Initialize DES with key
this .key = CryptoJS.enc.Hex.parse(key);
encrypt(plaintext) <
// Perform DES encryption on plaintext
const encrypted = CryptoJS.DES.encrypt(
// Return ciphertext as hex string
return encrypted.ciphertext.toString();
decrypt(ciphertext) <
// Parse ciphertext from hex string
const ciphertextHex = CryptoJS.enc.Hex.parse(ciphertext);
// Perform DES decryption on ciphertext
const decrypted = CryptoJS.DES.decrypt(
// Return decrypted plaintext as UTF-8 string
return decrypted.toString(CryptoJS.enc.Utf8);
Output
. 60AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536
Output:
Encryption:
After initial permutation: 14A7D67818CA18AD
After splitting: L0=14A7D678 R0=18CA18AD
Round 1 18CA18AD 5A78E394 194CD072DE8C
Round 2 5A78E394 4A1210F6 4568581ABCCE
Round 3 4A1210F6 B8089591 06EDA4ACF5B5
Round 4 B8089591 236779C2 DA2D032B6EE3
Round 5 236779C2 A15A4B87 69A629FEC913
Round 6 A15A4B87 2E8F9C65 C1948E87475E
Round 7 2E8F9C65 A9FC20A3 708AD2DDB3C0
Round 8 A9FC20A3 308BEE97 34F822F0C66D
Round 9 308BEE97 10AF9D37 84BB4473DCCC
Round 10 10AF9D37 6CA6CB20 02765708B5BF
Round 11 6CA6CB20 FF3C485F 6D5560AF7CA5
Round 12 FF3C485F 22A5963B C2C1E96A4BF3
Round 13 22A5963B 387CCDAA 99C31397C91F
Round 14 387CCDAA BD2DD2AB 251B8BC717D0
Round 15 BD2DD2AB CF26B472 3330C5D9A36D
Round 16 19BA9212 CF26B472 181C5D75C66D
Cipher Text: C0B7A8D05F3A829C
Decryption
After initial permutation: 19BA9212CF26B472
After splitting: L0=19BA9212 R0=CF26B472
Round 1 CF26B472 BD2DD2AB 181C5D75C66D
Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D
Round 3 387CCDAA 22A5963B 251B8BC717D0
Round 4 22A5963B FF3C485F 99C31397C91F
Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3
Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5
Round 7 10AF9D37 308BEE97 02765708B5BF
Round 8 308BEE97 A9FC20A3 84BB4473DCCC
Round 9 A9FC20A3 2E8F9C65 34F822F0C66D
Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0
Round 11 A15A4B87 236779C2 C1948E87475E
Round 12 236779C2 B8089591 69A629FEC913
Round 13 B8089591 4A1210F6 DA2D032B6EE3
Round 14 4A1210F6 5A78E394 06EDA4ACF5B5
Round 15 5A78E394 18CA18AD 4568581ABCCE
Round 16 14A7D678 18CA18AD 194CD072DE8C
Plain Text: 123456ABCD132536
Conclusion
In conclusion, the Data Encryption Standard (DES) is a block cipher with a 56-bit key length that has played a significant role in data security. However, due to vulnerabilities, its popularity has declined. DES operates through a series of rounds involving key transformation, expansion permutation, and substitution, ultimately producing ciphertext from plaintext. While DES has historical significance, it’s crucial to consider more secure encryption alternatives for modern data protection needs.
Frequently Asked Questions
Q.1 : What should be considered as an alternative to DES for data encryption?
Answer:
For modern data encryption needs, consider using stronger encryption algorithms like AES (Advanced Encryption Standard).
Q.2 : How is the 48-bit subkey generated for each round in DES?
Answer:
The 48-bit subkey for each round in DES is derived from the 56-bit key through a process of circular shifting and permutation, ensuring key diversity.








